How's this for an elegant proof of the extra element theorem. Let me know what you think.
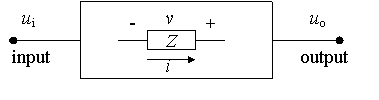
Add an extra element Z
between any two nodes in a linear system:
Treat i as a second input, and v as a second output:
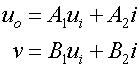 Eqn
1
Eqn
1
![]()
![]() Eqn
2
Eqn
2
Eliminate i, v.
Solve for![]() :
:
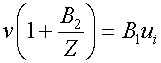
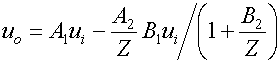
![]() Eqn
3
Eqn
3
This gives A(Z) in terms of the original transfer function A1, and three coefficients that can be determined from analysis of the system without Z connected. We can reduce these three unknowns to two, and put the equation in standard “bilinear” form with some additional algebra:
![]()
![]() (bilinear)
Eqn 4
(bilinear)
Eqn 4
where by definition:
![]() (denominator)
Eqn 5
(denominator)
Eqn 5
![]() (numerator)
Eqn 6
(numerator)
Eqn 6
These two unknowns look more complex than the previous three, but they have a simple interpretation, and they are often more easily determined. Also, the bilinear form has a nice interpretation when the original network has resistors only, and we are adding one reactive element Z. Adding this element multiplies the original transfer function with one pole and one zero.
The interpretation of the two new parameters is as follows:
![]()
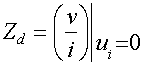 Eqn
7
Eqn
7
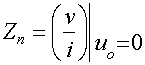 Eqn
8
Eqn
8
Zd is the impedance seen by element Z
when the input
is nulled (![]() in
eqn 1). Zn
is the impedance when the output is nulled (
in
eqn 1). Zn
is the impedance when the output is nulled (![]() in
eqn 1). The first
is obvious by inspection of eqn 1. The
second requires a little algebra to prove.
Note that the output is nulled by setting the proper ratio for
the two
inputs, not by simply placing a short on the output terminal. Shorting the output would result in a network
different than that specified by eqn 1.
in
eqn 1). The first
is obvious by inspection of eqn 1. The
second requires a little algebra to prove.
Note that the output is nulled by setting the proper ratio for
the two
inputs, not by simply placing a short on the output terminal. Shorting the output would result in a network
different than that specified by eqn 1.
As will be seen in the examples, the computation of Zn using eqn 8 in a real circuit is often simple, even though its definition (eqn 6) is more complex. This is because nulling the output often nulls other elements as well, and nulled elements don’t contribute to the impedance Zn.
I think our students get too bogged down in the math, and miss the
simple insights they need to become good desingers.