Cooking a Potato

After learning about the types of heat transfer, what equations are used to explain them, and how to use the equations, we are now ready to begin explaining how it all relates to our project. We will explain, by example, the heat transfer that goes on while baking a potato.

Problem:

A potato is placed in an oven at 350^oF. The potato was originally at room temperature of 70^o F. First find the amount of heat transferred, assuming the potato reaches 350^oF, then apply what we know to determine the time to cook the potato.

Solution:

Our first challenge is to understand what type of heat transfer is involved in this example. In the oven, the oven walls get hot. The movement of heat from the walls of the oven to the potato cooking inside the oven is radiant heat transfer. The heat is "radiating" from the walls of the oven to the potato. We also know that the heat is transferred through the air in the oven to the potato. The air in the oven moves, or circulates, naturally. This movement allows for the heat to also move. This movement of heat through the air in the oven is due to convection. Conduction is the third type of heat transfer. It is the transfer of heat between two touching solids. In this example, there is heat conduction between the wire oven rack that the food is sitting on and the potato itself. Since the wire oven rack is very small, or has a small solid area, then we are going to assume that it cannot transfer very much heat to the potato. The heat transfer through conduction will be much less than the heat transfer through radiation or convection, therefore we are only going to deal with heat convection and radiant heat transfer.

To find the total heat transfer, Q, we will find the radiant heat transfer, Q_r, and add it to the convective heat transfer, Q_c. The equation discussed for radiant heat was:

Q_r = -h_rA(T₁ – T₂)

In this example, the heat transfer coefficient was not given to us. When a constant is not given to us, we must find a way to calculate it. Therefore I looked in the "Fundamentals of Food Engineering" book by Stanley E. Charm and found the following equation for radiant heat transfer coefficients with the units of Btu/(hr*ft²*^oF).

h_r = 0.173 * e₁ * {[(0.01T₁)⁴ - (0.01T₂) ⁴] / [T₁- T₂]}

Emissivity is a ratio between the energy that is emitted from an object and the maximum amount of energy that could be emitted from an ideal object. Emissivity is a complicated subject. Description beyond this is not required here, but could be found in "Heat, Mass, and Momentum Transfer."

Let’s return to the baked potato example for a minute now. In the example,

Solving for the radiant heat transfer coefficient,

h_r = 0.173 * (0.9) * {[(0.01 * 70^oF)⁴ – (0.01 * 350^oF)⁴] / [70^oF – 350^oF]}

h_r = 0.083 Btu / (hr*ft²*^oF)

The next step in determining the amount of heat transfer in the baked potato is to determine the area of the potato. Let’s assume that we have a spherical potato with a diameter (length) of 4in. Recall when calculating area of a sphere, we use the following equation.

A = 4P *r²

Where r = radius of the potato, which is equal to half of the diameter

A = 4*P *(2in) ²

A = 50.3 in²

If we convert 50.3 in² to ft², knowing there is 144 in² for every square foot, we find that we have a potato with an area of 0.35 ft².

A = 50.3 in² * (1 ft² / 144 in²) = 0.35 ft²

Now that we know all of the variables in the heat equation, we can solve for the amount of radiant heat transfer by plugging the values into the original equation.

Q_r = -h_rA(T₁ – T₂)
Q_r = -(0.083 Btu / (hr*ft²*^oF) )*(0.075 ft²) * (70 ^o F - 350 ^oF)

We are not finished yet, though. We also know that there is heat traveling through the air to the potato. This describes heat convection, therefore we must find the heat due to convection. The convective heat transfer equation described earlier is represented below.

Q_c = -h_cA(T₁ – T₂)

Again, we were not given the convective heat transfer coefficient. Looking in the "Heat, Mass, and Momentum Transfer," I found the following equation that is applicable to our problem. It is a correlation that is generally acceptable for any heat transfer coefficients in a sphere.

h_cD / k = 2 or

h_c = 2*k / D

where h_c = the convective heat transfer coefficient

(I need a review of the above concepts)

In the book "Fundamentals of Food Engineering", the thermal conductivity of a raw potato was found to be 0.63 Btu / (h*ft*^oF). Plugging the thermal conductivity and diameter into the above equation, we can solve for the heat transfer coefficient, h_c.

h_c = 2*k / D

h_c = 2*0.63 Btu/(h*ft*^oF) / 0.33 ft

h_c = 3.82 Btu/(h* ft²*^oF)

Now that we know all of the variables in the heat equation, we can solve for the amount of convective heat transfer.

Q_c = -h_cA(T₂ – T₁)
Q_c = -(3.82 Btu / (hr*ft²*^oF) )*(0.35 ft²) * (70 ^o F - 350 ^oF)

We can now combine the two heats that we calculated and get the total rate of instantaneous heat transfer as:

Q = Q_c + Q_r = 374.4 Btu/hr + 1.75 Btu/hr

The heat transfer that we just solved for was the instantaneous (what happened at one time and one temperature) heat. This is not very interesting, because in reality, heat is accumulating in the potato. This steady buildup of heat in the potato is referred to as unsteady-state heat transfer. Dealing with the unsteady-state heat transfer allows us to relate time to the equations. It deals with questions such as, "How long will it take the potato to cook?" This is obviously a more interesting question. After all, how often are you cooking and ask yourself, "How much heat is being transferred into my food?" I know, never. On the other hand, how often have you been cooking and asked yourself, "How long do I have to leave this in the oven for?" This is a much more common question.

Problems involving time are much more difficult than the ones without. I could present a series of complicated equations, compare and contrast them, altering them slightly while making many assumptions, and then come up with the answer to the simple question, "How long do I have to cook the potato for?" This would take a lot of work for such a simple problem. Instead of torturing ourselves, many scientists have done this exact thing and come up with some simple graphs that we can use to lower our workload. The graphs make answering such a simple question much more reasonable. The figure below is one of these graphs for spherical objects. I will explain what the variables are and how to use them, but will not go into any unneeded information about the graphs. If you are interested in how the graph was formulated, or why it works, please reference "Heat, Mass, and Momentum Transfer" or another heat transfer textbook for more information.

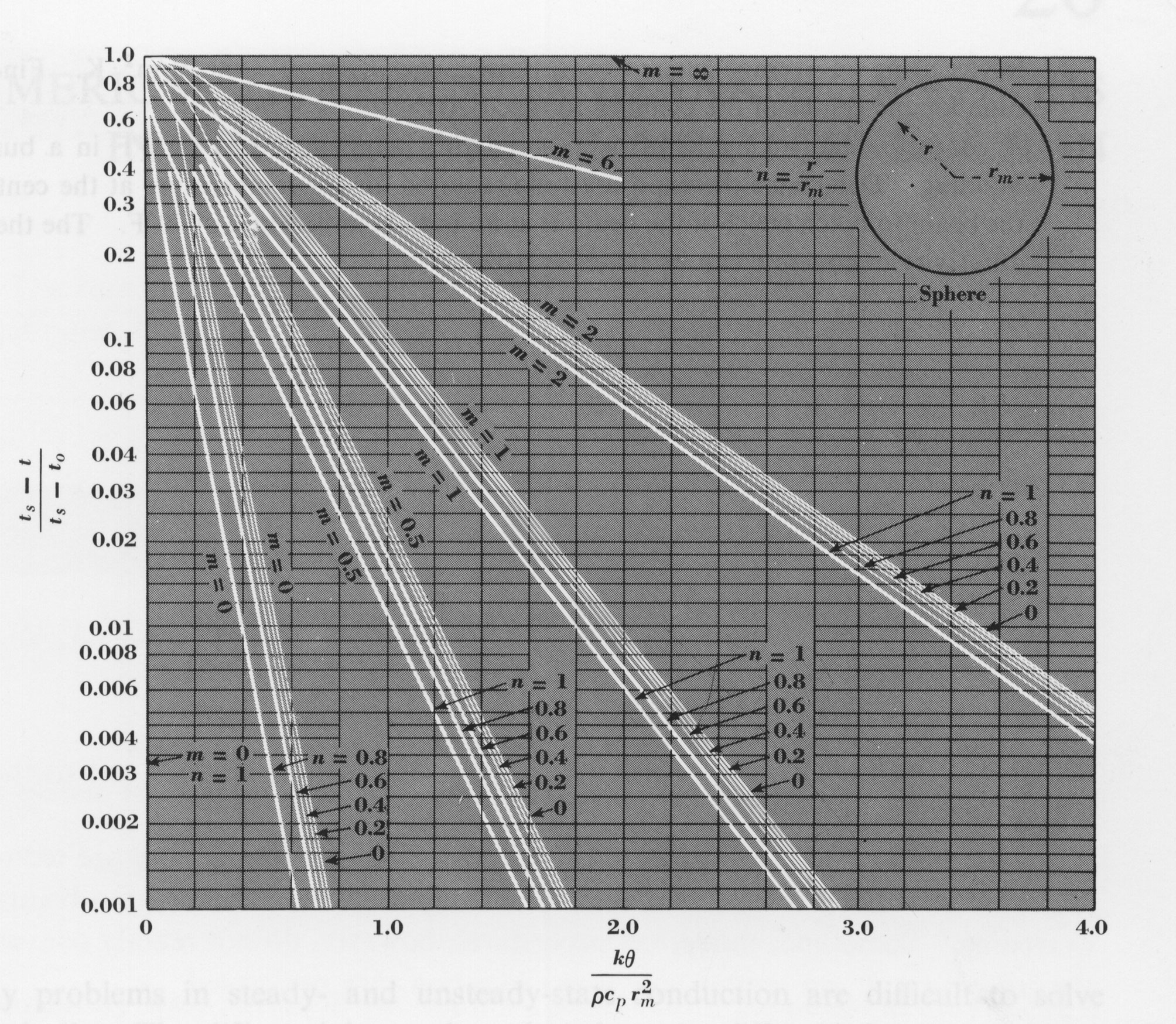
The graph introduces many variables. I will try to define each of them now.

• T_a = the temperature inside the oven (units: ^oF)
• T = the temperature at a certain time, Q, (units: ^oF)
• T_b = the initial temperature of the potato (units: ^oF)
• r = the distance from the center of the potato to the point being measured (units: ft)
• r_m = the radius of the potato ( ˝ the diameter), (units: ft)
• n = r / r_m (no units)
• h = the convective heat transfer coefficient (units: Btu / (h*ft²* ^oF))
• k = the thermal conductivity of the potato (units: Btu / (h*ft* ^oF))
• m = K / (r_m*h), (no units)
• r = density of the potato (units: lb / ft³)
• Q = time of heating in the oven (units: h)

(I need a review of the constants)

• C_p = the heat capacity of the potato - The heat capacity of a potato can be defined as the capacity the potato has to hold heat. Capacity means the maximum amount possible. Therefore, heat capacity is a constant that describes the maximum amount of heat that a potato can hold. The "Fundamentals of Food Engineering" book quotes the heat capacity of a potato to be 0.84 Btu / (lb*^oF).

We have already discussed many of the values for these variables. We know the following:

Now let’s discuss what variables we do not already know. T, the temperature at a certain time, Q, is going to be the temperature that the potato needs to get to in order to be cooked thoroughly. To find this final temperature, I baked a potato at 350 ^oF and stuck a thermometer into the center of it when it was done. I found this final temperature of the cooked potato to be 340 ^oF. We will therefore set T = 340 ^oF. It is also evident that we want the center of the potato to reach 340 ^oF because if it doesn’t then the potato will not be cooked in the center. Since we want to be measuring the temperature at the center of the potato, and r is the variable representing the distance from the center that we are measuring temperature, we will set r = 0 feet. Then, by definition of n (n = r / r_m), n must also be zero. Let’s summarize:

Now our only unknown variable is time, Q, therefore we can use the graph to find time by using all the information that we already know. Let’s do this process in steps:

Y = (T_a – T) / (T_a – T_b)

Y = (350 – 340) / (350 – 70)

Y = 0.036

X = k*Q / (r *C_p*r_m²)

0.45 = k*Q / (r *C_p*r_m²)

Q = 0.45*r *C_p*r_m² / k

Q = 0.45* 61lb/ft³ * 0.84Btu/(lb*^oF) * 0.167²ft² / 0.63Btu/(h*ft* ^oF)

Q = 1.0 hrs

Next time you are baking a potato, you now know that it will be thoroughly cooked if you bake it at 350^oF for one hour. I bet you never expected so much engineering and science to be involved in such a simple task as baking a potato. Next time you are in the kitchen, think to yourself, "What is going on with this process?" Chances are, you may know the answer.