Problem 14.5

a)

We will make a table of each function, it's AR plateau, its break frequency (w_b), and slope.

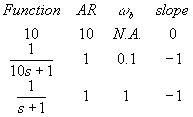
where N.A. means that there is no break frequency. In general,

f for 10 = tan^-1(0/10) = 0^o

f for 10s+1 = tan^-1(10w/1) = tan^-1(10w)

f for s+1 = tan^-1(w/1) = tan^-1(w)

f total = 0 - tan^-1(10w) - tan^-1(w)

We must calculate AR_total and f_total, which is shown in the table below:

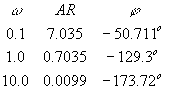
The asymptotic plot is shown below (note that we were only asked to plot AR and not f):

b)

We will make a table of each function, it's AR plateau, its break frequency (w_b), and slope.

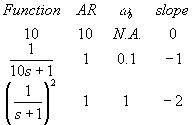
where N.A. means that there is no break frequency. In general,

f for 10 = tan^-1(0/10) = 0^o

f for 10s+1 = tan^-1(10w/1) = tan^-1(10w)

f for (s+1)² = 2tan^-1(w/1) = 2tan^-1(w)

f total = 0 - tan^-1(10w) - 2tan^-1(w)

We must calculate AR_total and f_total, which is shown in the table below:

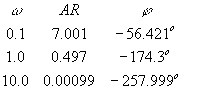
The asymptotic plot is shown below (note that we were only asked to plot AR and not f):

c)

We will make a table of each function, it's AR plateau, its break frequency (w_b), and slope.

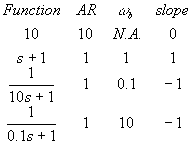
where N.A. means that there is no break frequency. In general,

f for 10 = tan^-1(0/10) = 0^o

f for s+1 = tan^-1(w/1) = tan^-1(w)

f for 10s+1 = tan^-1(10w/1) = tan^-1(10w)

f for (0.1s+1) = tan^-1(0.1w/1) = tan^-1(0.1w)

f total = 0 + tan^-1(w) - tan^-1(10w) - tan^-1(0.1w)

We must calculate AR_total and f_total, which is shown in the table below:

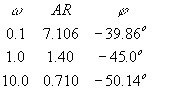
The asymptotic plot is shown below (note that we were only asked to plot AR and not f):

d)

We will make a table of each function, it's AR plateau, its break frequency (w_b), and slope.

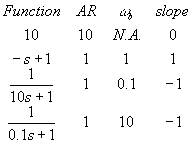
where N.A. means that there is no break frequency. In general,

f for 10 = tan^-1(0/10) = 0^o

f for -s+1 = tan^-1(-w/1) = tan^-1(-w)

f for 10s+1 = tan^-1(10w/1) = tan^-1(10w)

f for (0.1s+1) = tan^-1(0.1w/1) = tan^-1(0.1w)

f total = 0 - tan^-1(w) - tan^-1(10w) - tan^-1(0.1w)

We must calculate AR_total and f_total, which is shown in the table below:

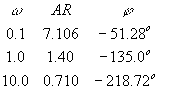
The asymptotic plot is shown below (note that we were only asked to plot AR and not f):

e)

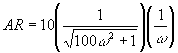
f for 10 = tan^-1(0/10) = 0^o

f for s = tan^-1(w/0) = tan^-1(infinity) = 90^o

f for 10s+1 = tan^-1(10w/1) = tan^-1(10w)

f total = 90^o - tan^-1(10w)

We must calculate AR_total and f_total, which is shown in the table below:

The asymptotic plot is shown below (note that we were only asked to plot AR and not f):

f)

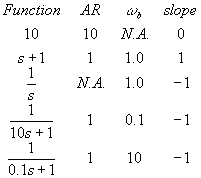
f for 10 = tan^-1(0/10) = 0^o

f for s+1 = tan^-1(w/1) = tan^-1(w)

f for s = tan^-1(w/0) = tan^-1(infinity) = 90^o

f for 10s+1 = tan^-1(10w/1) = tan^-1(10w)

f for (0.1s+1) = tan^-1(0.1w/1) = tan^-1(0.1w)

f total = tan^-1(w) - 90^o - tan^-1(10w) - tan^-1(0.1w)

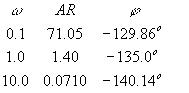
The asymptotic plot is shown below (note that we were only asked to plot AR and not f):